![]() DEPARTMENT OF MECHANICS AND APPLIED MATHEMATICS
DEPARTMENT OF MECHANICS AND APPLIED MATHEMATICS
THE FRACTAL MODEL OF THE BLOOD-VESSEL SYSTEM
HEAD OF THE PROJECT Jaan KALDA, Ph.D., senior researcher
DESCRIPTION
The aim of the project is to elaborate a fractal model of the blood-vessel network as a whole, which would be in agreement with the current understanding of the processes governing the growth of the vascular network and with the empirical data.
Let us make a rough estimate of the similarity dimension of the blood-vessel tree. We can use the following empirical data: the length of the capillaries (i.e. the vessels of the last generation)
![]()
![]()
![]() 0
0
![]() 0.5
0.5![]() 0.5 m
0.5 m![]()
![]() 0N
0N
![]() 100,000 km
100,000 km![]() 0/
l0)1/neff
0/
l0)1/neff
Ds = -1/ log2a
![]() 3.4
3.4
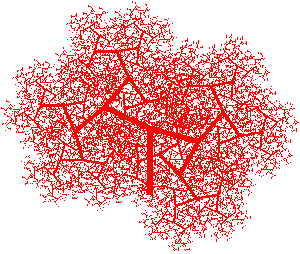
The fractal model of the blood-vessel system with Ds
The seemingly curious fact that the similarity dimension exceeds the topological dimension can be explained as follows. The Hausdorff-Besicovitch and box-counting dimensions of a space-filling fractal set
![]() D
D
ESF GRANTS
- No 902 (1996-1998)
PUBLICATIONS and TALKS at CONFERENCES
- Kalda J. On the optimization of Monte-Carlo simulations. - Physica A, 1997, 246 - 646-658.
- International Conference on the Unity of the Sciences, Washington, 24.-29. November 1997.
Jaan Kalda: "On the Modelling of Fractal Tree-like Structures in Biology".
- 5th Int. Conf. Fractal 98, (forthcoming)
J. Kalda, "Fractality of the blood-vessel system: the model and its applications"
![]()
![]()
![]() 07/04/1998 webmaster
07/04/1998 webmaster